I løpet av de siste dagene har jeg oppdaget at koordinater er noe svineri. Ikke alle typer koordinater, naturligvis. Kartesiske koordinater er fine. Det er noe man kan forholde seg til. Polarkoordinater også, og sylindriske, sfæriske, toriodale (eller smultringske, som det heter på norsk), alt dette kan man forholde seg til. Og krummet rom og Riemann og greier, bring it on. Så lenge man har en grei metrikk å forholde seg til, sånn at alle er enige om hva som foregår.
Nei, den typer koordinater jeg snakker om er slike som forteller deg hvor landet ligger, bokstavelig talt. Jeg er en uskyldig ung mann, og så langt har jeg levd et beskyttet liv, forskånet for denslags. Men så, brått og uten forvarsel, ble jeg nødt til å kikke på et datasett med havstrømmer, og jeg oppdaget at alle slett ikke er enige om hvor landet ligger. «Men Aha!» sier du kanskje, hvis du er som meg, «Det er da for pokker bare å bli enige om hvor sentrum av Jorden ligger, så kan man unikt definere alle punkter på overflaten med én breddegrad og én lengdegrad (om vi ser bort fra grotter, og fjellvegger som heller utover og andre marginale tilfeller der flere enn ett punkt kan ha samme koordinater). Ferdig arbeid. La oss lage en kanne kaffe og feire.»
Det viser seg imidlertid at for det første er det ikke helt trivielt å definere Jordens sentrum, skjønt der later man til å ha gjort en god jobb, og funnet et punkt der, i følge wikipedia, «
the error is belivied to be less than 2 cm». Høres bra ut, men det viser seg at det andre problemet er at man også trenger å være enige om hvilken fasong Jorden har for å unikt definere et punkt på denne måten, og Jorden, viser det seg, har en irriterende komplisert fasong. For å ta et helt konkret eksempel på hva dette kan bety, ta en kikk på dette kartutsnittet av en eller annen tilfeldig fjord på Grønnland.
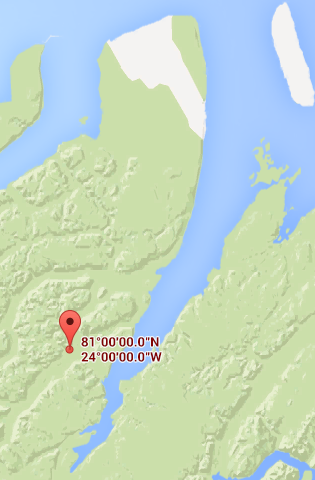
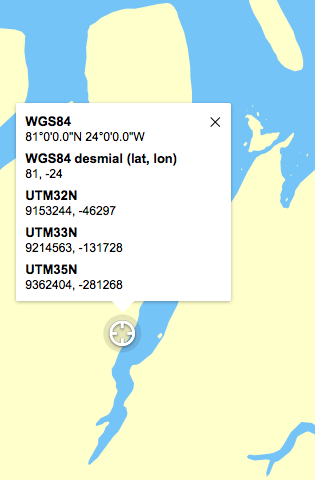
Til venstre, Google Maps, til høyre, Gule sider.
Det viser seg altså at Google Maps og Gule sider slett ikke er enige om hvor denne fjorden ligger. Og det er ikke så enkelt som at de er like uenige overalt heller. Her er et annet eksempel, denne gangen fra en liten øy på Svalbard:
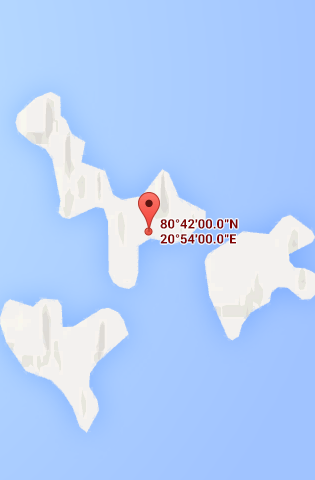

Til venstre, Google Maps, til høyre, Gule sider.
Dette er omtrent like langt nord, men noe lengre øst, og her er altså de to temmelige enige om koordinatene. Funky greier.
Merk forøvrig at dette er et annet problem enn det som har med kartprojeksjoner å gjøre. Kartprojeksjoner handler om å legge vekt på det ene eller det andre når man må gjøre tilpasninger for å vise noe som ikke er flatt i utgangspunktet på et flatt kart, men ulike kartprojeksjoner er i bunn og grunn bare ulike visninger av de samme dataene.
Dette er altså slike problemer jeg ikke har trengt å forholde meg til tidligere, men når man plutselig får et datasett med havstrømmer, og det viser seg at to ulike programmer ikke er enige om hvorvidt det faktisk er hav der, blir det straks relevant å vite litt mer om hvordan ting henger sammen.
I morgen: Vi tegner data på kart med python.
Anders K. likes this





Comments