Dimensjonsanalyse er et meget anvendbart triks fysikere ofte bruker. Det første det kan brukes til er å sjekke om noe du har regnet ut virker rimelig, ved å sjekke om enhetene stemmer. For eksempel, hvis man skal finne kraften fra eller på et eller annet, forventer man å få et svar i enheten Newton. Ja, jeg vil faktisk gå så langt som å si at hvis man får noe annet er svaret feil. Med mindre man får Joule per meter, som faktisk er det samme som Newton. Dere skjønner sikkert hva jeg mener. Får man et svar i meter per sekund er det i alle fall bombesikkert at det man har gjort er galt. Slik kan dimensjonsanalyse brukes til å vurdere riktigheten av et svar man har regnet ut.
En annen ting det kan brukes til er å sjekke riktigheten av et svar man ikke har regnet ut. For eksempel på en flervalgsprøve vil det noen ganger være slik at enkelte av alternativene har feil enheter, og da kan man lett utelukke dem. Dette funker naturligvis bare hvis faglæreren enten ikke har tenkt over saken, eller har lagt opp til at man skal bruke dimensjonsanalyse for å gjøre livet lettere for de smarte studentene.
Dimensjonsanalyse kan også brukes til å finne ut nye og spennende ting. For eksempel, den eneste måten å kombinere fundamentale naturkonstanter på en slik måte at resultatet får dimensjon lengde er
Man er ikke helt sikker på hva denne lengden er, men sannsynligvis er den viktig i noe kvantegrafs. Kanskje er det på denne lengdeskalaen rommet begynner å bli dominert av kvanteeffekter slik at det ikke er glatt og fint lengre? Kanskje har det noe med kvantegravitasjon å gjøre? Hvem vet. Men det er i alle fall spennende, og det falt rett ut av dimensjonsanalyse.
-Tor Nordam

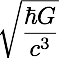
Comments