Her om dagen var jeg på et lite introkurs i parallellprogrammering rettet mot superdatamaskiner. Det varte bare et par timer, og jeg går dessverre glipp av de to neste kursene, som går litt mer i detalj på OpenMP og MPI, og dessuten et tredje kurs om avansert bruk av Njord, men det var interessant likevel. Mannen som holdt kurset presenterte to lover som gjerne trekkes fra i sammenheng med parallellprogrammering, nemling Amdahls lov, og Gustafsons lov.
Amdahls lov, oppkalt etter norsk-amerikaneren Gene Amdahl, sier noe om hvor stor hastighetsøkning du kan få på programmet ditt ved å parallellisere det. Hvis vi sier at
P er den andelen av programmet som lar seg parallellisere, mens resten av programmet, som da blir 1-
P, ikke lar seg parallellisere, kan du i beste fall få en hastihetsøkning på
der
N er antall kjerner du kjører på. Så hvis for eksempel 10% av programmet ditt ikke lar seg parallellisere, vil du aldri kunne få en hastighetøkning på mer enn en faktor 10, uansett hvor stor datamaskin du har. Amdahls lov fremstår i grunnen som sunn fornuft hvis man tenker litt over det, og sant å si synes jeg kanskje det var litt billig for å få en lov oppkalt etter seg, men noe må man jo kalle den, og det var ikke akkurat som om jeg kom opp med det først.
Gustafsons lov, oppkalt etter John Gustafson, tar et litt annet utgangspunkt. Den antar at etterhvert som tilgjengelig datakraft øker vil forskere ikke bruke kortere tid på å løse problemene sin, men derimot øke størrelsen på problemene slik at de fremdeles tar omtrent like lang tid. Hastighetsøkningen, som man da definerer ved å sammenligne med tiden det ville tatt å kjøre det samme programmet på en maskin med én kjerne, blir
Der
N er antall kjerner, og 1-
P er den delen av programmet som ikke lar seg parallellisere, som man antar er like stor hele tiden.
Kursholderen påpekte forøvrig det morsomme poenget at Amdahls lov gjelder for doktorgradstudenter, for vi vil helst bli ferdige med problemene våre så fort som mulig, mens Gustafsons lov gjelder for professorer, for de har ikke så mye tidspress, og vil heller bruke like lang tid som før men produsere bedre data. Og så begynte han på en historie om en student som hadde kommet til superdatamaskinfolkene og vært helt panisk fordi hun hadde seks uker igjen av doktorgraden, og programmet hennes tok altfor lang tid, og jeg forventet naturligvis at han skulle fortelle om hvordan de hadde tatt enkle grep og gjort programet massivt parallelt og dermed reddet dagen, men, sa han, med en liten latter, på seks uker var det naturligvis ingenting de kunne gjøre. Huffda.
-Tor Nordam

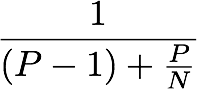
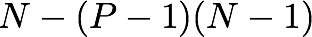
Comments