Det kom en student bort til meg en dag, og spurte hvorfor det er slik at man bare kan brette et ark sju ganger. Jeg ble litt overrasket, da jeg ikke egentlig har tenkt på dette som et fysikkspørsmål før, men det er det jo naturligvis. Uansett, svaret er åpenbart at det ikke finnes noen slik grense.
Poenget er, i fall noen ikke kjenner problemet, at du tar et ark og bretter det i to på midten flere ganger. Med vanlig tilgjengelige ark vil du typisk bare greie å brette arket sju ganger. Årsaken er naturligvis at arealet halveres hver gang du bretter, mens tykkelsen dobles, eller gjerne mer enn dobles, på grunn av ikke-lineære effekter eller hva man skal kalle den knørvingen som typisk oppstår når du har brettet noen ganger.
Når du har brettet 7 ganger har du økt tykkelsen med en faktor 2
7=128, mens du har redusert arealet med samme faktor, altså til under en prosent av den opprinnelige størrelsen. For et vanlig ark, som et A4-ark, eller til og med et A3-ark om man skulle ha noe slikt liggende, har du da typisk endt opp med noe som er for lite og for tykt til å kunne brettes.
Det er imidlertid lett å se at dette ikke er en universell regel. Systematiske forsøk, det vil si bretting av gamle forelesningsnotater, indikerer at hvis man bretter et A4 ark 7 ganger ender man opp med noe som er ca 2x3 cm, og 1,5 cm tykt. Hvis man derimot hadde begynt med et ark som var mye større, for eksempel 2x3 meter, men av samme tykkelse, ville man etter 7 brettinger ende opp med noe som var ca 20x30 cm, og fortsatt 1,5 cm tykt, eller gjerne litt tynnere fordi man får penere bretter med større ark. Et slikt objekt burde det ikke være problematisk å brette en, eller kanskje to ganger til. Og hvis man virkelig er ivrig kan man lage mye større og tynnere ark, for eksempel ved å lime sammen tusenvis av sigarettpapir, og egentlig brette så mange ganger man ønsker.
Så hvor mange ganger kan man egentlig brette et ark? Mine begrensede data tilsier at man kan ikke brette lenger når forholdet mellom tykkelse og lengde er omtrent 0,5. Med litt triksing og miksing og liberal avrunding finner vi da at antall brett kan uttrykkes som en funksjon av tykkelse og lengde. Hvis du har et ark med tykkelse
d og lengde
L, kan du brette arket
N ganger, der
Jeg har her antatt at arket er sånn passe normalt formet, det vil si at ingen av sidene er mer enn dobbelt så lang som den andre.
For et vanlig A4-ark, med
L=300 mm, og
d=0,1 mm, gir formelen min at vi kan brette 7,3 ganger, som stemmer bra, så nå tror jeg at jeg bare lager meg en kopp te og setter meg til å vente på en
ig Nobel-pris.
-Tor Nordam

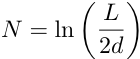
Comments