Den handelsreisendes problem
Tenk deg at du er en handelsreisende, og at du bor i for eksempel Oslo. Du har en liste med byer du skal besøke, hvorpå du skal returnere til Oslo. Du lever i tiden og forventer effektivitet, og ønsker derfor å finne den korteste ruten som tar deg innom alle byene og tilbake til utgangspunktet. Den enkleste tilnærmingen til dette problemet er naturligvis å lage en liste over alle mulige reiseruter, og deretter regne ut hvor lange de er, og finne den som er kortest. Problemet med denne fremgangsmåten er at med N byer finnes den N! ulike ruter, og dette blir ganske raskt en uhåndterlig størrelse.
For noen år siden ble dette problemet gitt til eksamen i Numerisk fysikk, der det var 15 byer som skulle besøkes. Det var med andre ord 1307674368000 mulige ruter, og bare det å generere listen over de ulike reiserutene med en vanlig datamaskin ville antagelig ta lengre enn hele eksamenstiden. Hvis man ser på problemet med 80 byer begynner antall mulige reiseruter å bli omtrent på størrelse med antall protoner i universet, og det blir raskt værre. Like fullt er det noen som har greid å løse dette problemet med 89500 byer. Det er åpenbart at her må man ty til sleipe triks.
Jeg brukte et par timer på dette problemet for noen dager siden, og jeg skrev et program som finner en tilnærmet løsning for et par tusen byer på bare noen få minutter. Jeg gikk frem som følger:
Først lager programmet en tilfeldig reiserute. Så ser det på to tilfeldige etterfølgende byer på ruten, og bytter rekkefølgen på dem. Hvis dette førte til at ruten ble kortere beholder vi den nye rekkefølgen, hvis ikke bytter vi tilbake. Så gjør man dette ca ti ganger så mange ganger som det er byer, og da begynner det å bli ganske bra. Figuren viser den totale lengden etter hvert skritt i programmet:
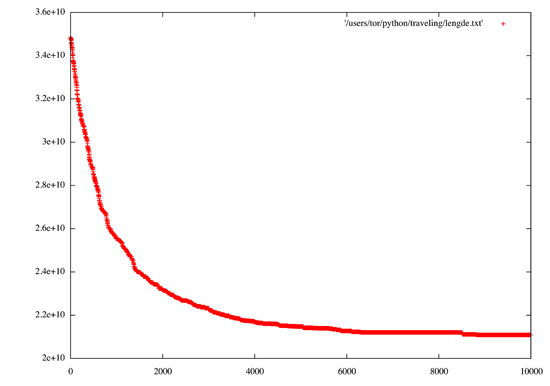
Som vi ser later det til at vi nærmer oss en løsning, men med en sleip juksemetode som dette kan man aldri være sikker på når man har den riktige løsningen. Det finnes imidlertid enda sleipere triks, som finner nøyaktige løsninger på rimelig tid. De har jeg imidlertid ikke satt meg inn i, men spesielt interesserte kan lese mer på wikipedia.
-Tor Nordam


Comments