I dag skal jeg skrive en artikkel om ganske barsk fysikk. Jeg skal dessuten stjele mye av det jeg har tenkt å si fra den fantastiske boken
Quantum Field Theory in a Nutshell. Jeg skal imidlertid prøve å gjøre det lettfattelig, og jeg vil også legge til at jeg gjengir fritt etter hukommelsen, så det er ikke som om jeg setter meg ned og oversetter noe noen andre har skrevet. Bare nesten.
Men først noen ord om boken. Til tross det lett spøkefulle navnet på en forholdsvis solid bok (hvis jeg hadde skrevet på engelsk ville jeg kalt den en «hefty tome»), er innholdet seriøst nok. Det er riktignok skrevet i en lettere tone enn de fleste bøker om kvantefeltteori, men den later faktisk til å være en mer eller mindre komplett innføring, og jeg tror forfatteren bruker den som lærebok når han underviser temaet. I det hele tatt har jeg bare pene ting å si om denne boken, bortsett fra at jeg blir litt skiplet av at han refererer til Richad Feynman som «Dick».
Det denne boken begynner med, noe som er litt unormalt, er veiintegral. Og det er det jeg skal skrive om i dag. Det høres fryktelig teknisk ut, og det er det vel egentlig også, men hold ut litt til. Denne boken forteller nemlig en helt fantastisk historie om veiintegralets opprinnelse.
Vi begynner med å se for oss det klassiske dobbeltspalteeksperimentet. Vi sender ut en strøm av partikler, som først treffer en skjerm med to små hull i, og deretter en detektor. For å finne sannsynligheten for at en partikkel treffer i et gitt punkt på detektoren må vi enkelt og greit legge sammen amplitudene fra de to hullene. Hele resten av historien bygger på dette poenget, så bruk gjerne litt tid på å tenke over dette.
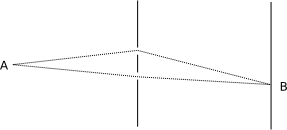
Når vi har blitt komfortable med to spalter, stiller vi det åpenbare spørsmålet, hva om vi borret et tredje hull? Vel, da ville vi måtte legge til amplituden fra det hullet også. Logisk nok. Og hva om vi la til en ekstra skjerm, og borret et par hull i den også? Vel, da ville vi ha 3 x 2 = 6 mulige veier å gå, og vi måtte legge sammen amplitudene fra hver av dem. Henger dere fortsatt med?
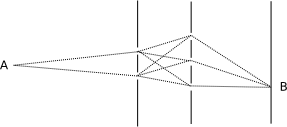
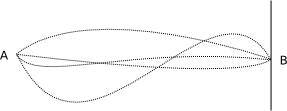
Nå kommer vi nemlig til det springende punktet. Boken forteller nemlig at det var her Feynman sa «Men hva hvis vi legger til uendelig mange skjermer, og så borrer vi uendelig mange hull i hver skjerm?». Vel, det åpenbare svaret er at man da må summere over amplitudene til uendelig mange mulige veier å gå. Men samtidig, når vi borrer uendelig mange hull i en skjerm vil det jo ikke være noen skjerm igjen. Så for å finne sannsynligheten for at en partikkel skal gå fra A til B i tomt rom kan vi altså legge sammen sannsynlighetene for alle mulige veier fra A til B. Er det ikke vakkert?
-Tor Nordam




Comments