I dag skal jeg bruke vanskelige ord om noe alle vet, nemlig at det er umulig å få en blyant til å balansere på spissen. Eller, det er ikke egentilg umulig, det er bare latterlig vanskelig, men vi skal late som om vi har en perfekt spisset blyant, og et perfekt hardt og flatt underlag, og at det faktisk er umulig å få blyanten til å balansere.
Det som skjer er altså at vi setter opp blyanten, og siden vi er så utrolig flinke og stødige karer står blyanten helt rett opp. Og så velter den. La oss se litt nærmere på det som skjer. Blyanten står altså rett opp og ned. Underlaget er helt flatt, og dessuten vannrett, selv om jeg glemte å nevne det, og tyngdekraften, som er den siste tingen som virker inn på systemet vårt, virker også rett nedover. Vi har med andre ord det som kalles et symmetrisk system, altså et system som ser likt ut fra alle kanter. Vi sier at systemet er rotasjons-invariant. Det er umulig å forutsi hvilken vei blyanten vil dette.
Likevel vet vi at blyanten detter, og når den gjør det, må den nødvendigvis dette i en eller annen retning. Etter at blyanten har falt har systemet vårt fått en retning, nemlig den veien blyanten veltet. Systemet vårt er ikke lenger symmetrisk.
Grunnen til at blyanten veltet, er at den har lavere energi når den ligger flatt på underlaget, enn når den står balansert på spissen. Det spiller imidlertid ingen rolle hvor på underlaget blyanten ligger. Den har den samme energien uansett.
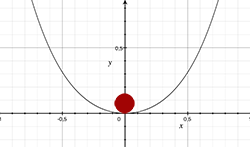
Vi kan tenke oss en lignende situasjon, der vi har en ball som vi legger i en skål. Hvis skålen har vanlig u-form, altså at den er lavest i midten, er det åpenbart at ballen vil legge seg i midten av skålen. Det er kanskje ikke alle som har tenkt over det, men det er fordi det er der den har lavest potensiell energi. Hvis ballen beveger seg bittelitt til siden, må den også bevege seg oppover, og det kan den ikke gjøre av seg selv. Det er det vi kaller en stabil likevekt.
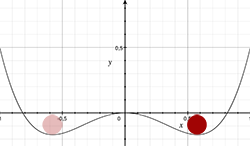
Hvis vi derimot ser for oss at skålen har en liten topp i midten, som vi så legger ballen på, har vi det som kalles en ustabil likevekt. Hvis ballen blir bittelitt forskjøvet vil den begynne å rulle raskere i den retningen. Dette er akkurat det samme som blyanten som balanserer på spissen. Til tross for at systemet i utgangspunktet er aldeles symmetrisk, vil det ende opp med en eller annen retning. Slike situasjoner som dette, når et system som i utgangspunktet er symmetrisk må velge en eller annen retning for å komme i en tilstand med lavere energi, er det vi fysikere kaller en spontant brutt symmetri.
Hvis den brutte symmetrien er global, gir dette opphav til masseløse eksitasjoner i feltet. Disse eksitasjonene kalles Goldstone-bosoner. Hvis systemet vi ser på derimot er invariant under en lokal SU(2)xU(1) gauge-transformasjon, og SU(2)-symmetrien er brutt på en passende måte, gir dette bruddet opphav til et masseløst boson som viser seg å være fotonet, og tre massive bosoner som viser seg å være W
+, W
- og Z
0. Så dikter vi opp enda et felt, som vi kaller Φ eller σ, alt ettersom, og så dukker Higgs-bosonet opp, og leptonene får masse, og alt ordner seg.
Jeg har eksamen i dette på fredag. Sympati plz.
-Tor Nordam


Comments